I started with a 3D pendulum system, the pendulum has massless string of length $l_1$ tied to the ceiling and a point mass $m_1$on the other end as shown in Figure 1. This is a pretty good approximation if you imagine a small bottle of ink held by a string tied to a fixed point. The idea is that there is a slow leak in the ink that is falling onto plane $A$ below, which is parallel to the xy plane. Plane $A$ is where the magic occurs, you could imagine $A$ is a piece of paper. I will refer to this pendulum system as "System 1".

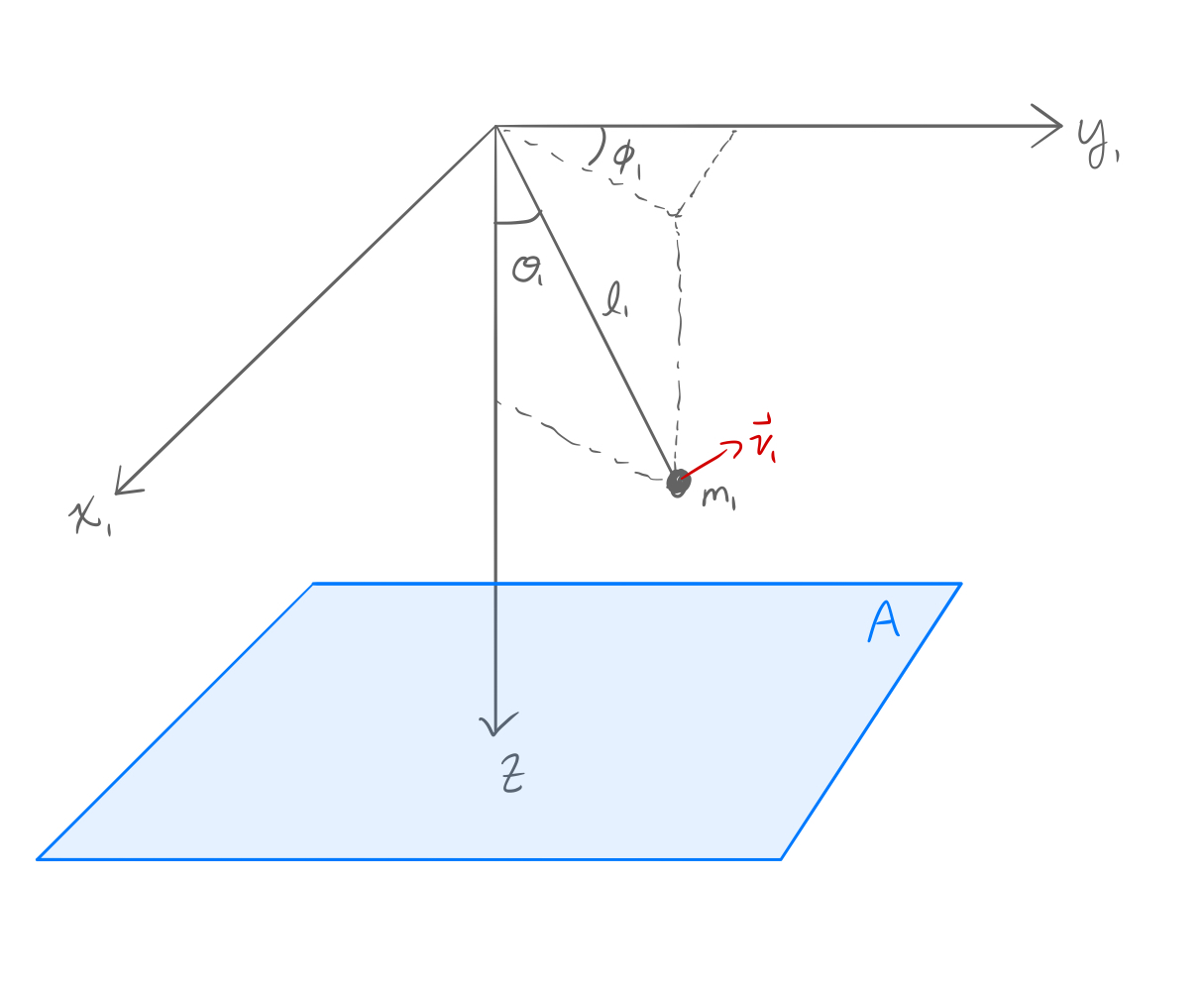
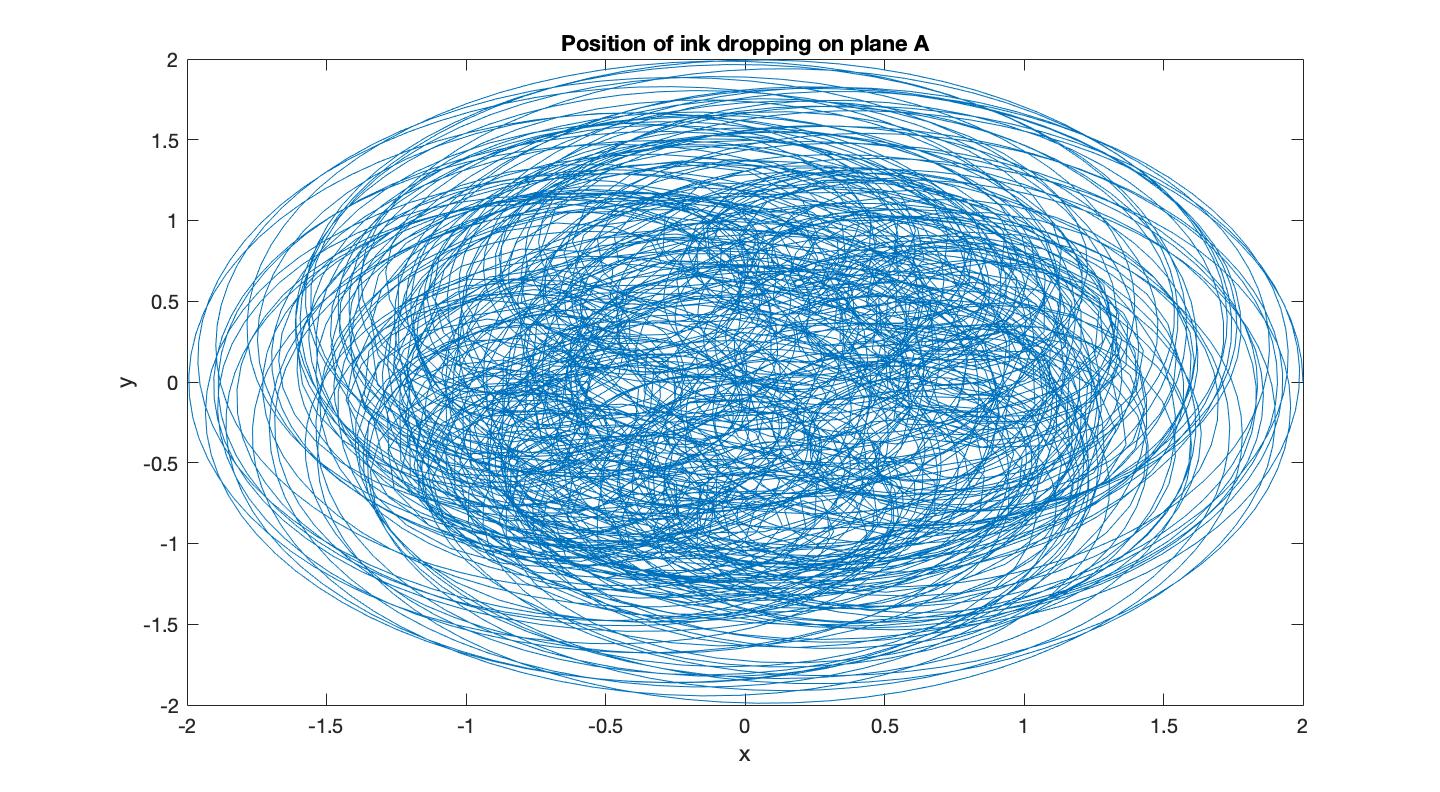
If we give the mass some initial velocity $\vec{v_o}$, and an initial position $\vec{r_o}$, we can then solve for the motion of $m_1$ using Lagrangian mechanics. This motion will produce a pattern due to the leaking ink hitting the plane $A$. I neglected the velocity of the ink leaving the bottle for simplicity sake, and took the projection of the position of $m_1$ onto plane A to be the position where the ink falls. Air friction was also neglected.

Now, this will form a pretty boring picture of concentric ellipses on plane $A$. To make things more interesting I tied plane $A$ to the top side of a second pendulum of length $l_2$ to the pivot point $O$ with mass $m_2$ on one end, and length $l_3$ from $O$ to point $P$ which is the origin of plane $A$ as shown in figure 3. The mass of plane $A$ is assumed to be zero here, which you could image if it were a piece of paper. Also $A$ is assumed to be kept parallel to the xy-plane at all time, one could enforce this with a ball joint and some control. I will call this pendulum system, "System 2".

The full system can be seen in figure 3. This system is how I was able to produce the interesting image at the top of the article.

I will solve each system independently, and as it turns out I will only need to solve System 1 as the result will generalize for System 2.

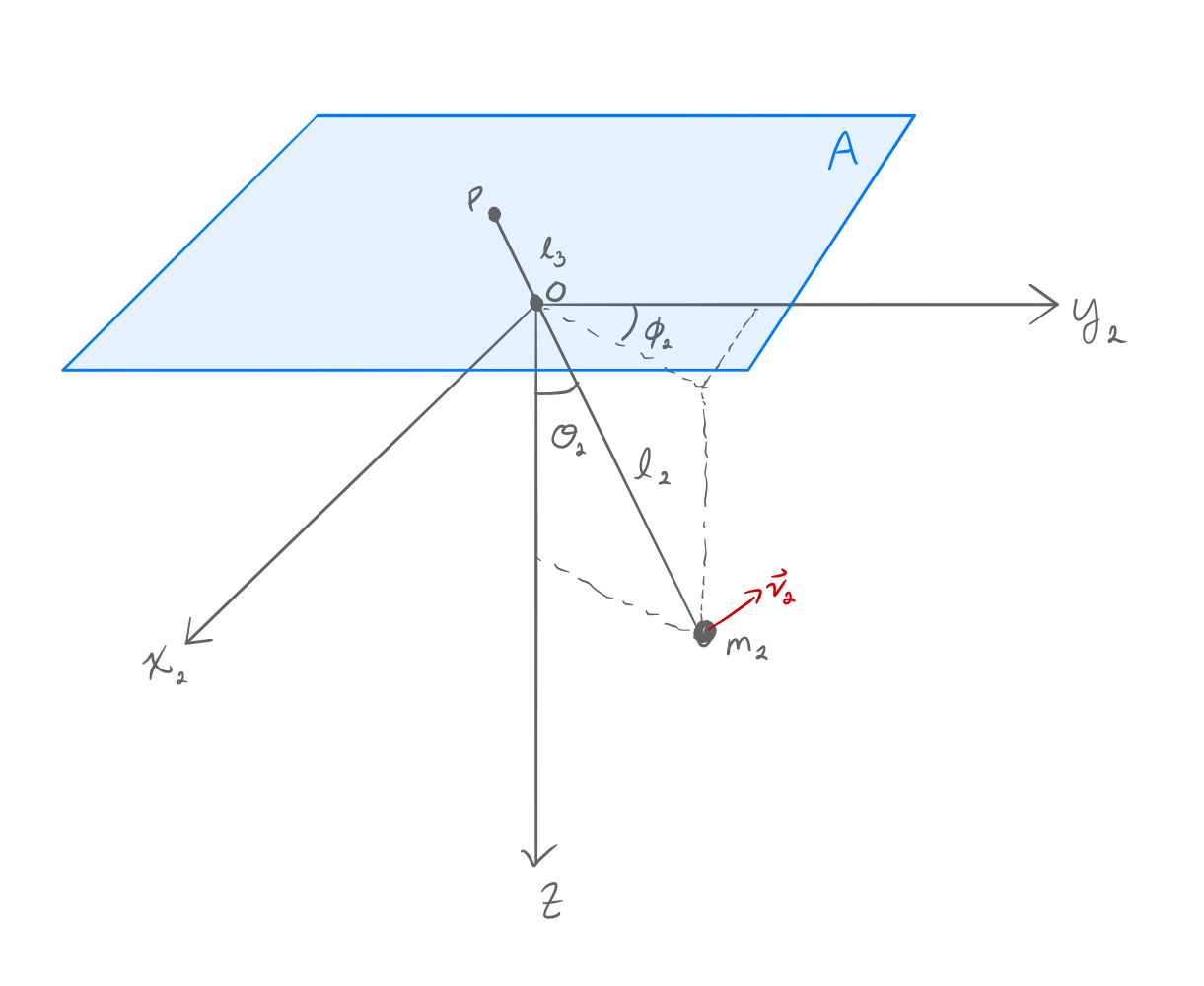
Start by noting there are 2 degrees of freedom ($s=2$), I will pick my generalized coordinates to be $\mathbf{q}=(\theta, \phi)$, note that because the results from System 1 will be the same as that from System 2 I will not use the subscripted angles. Writing the cartesian position in terms of $\mathbf{q}$ we have (where the dot above implies the time derivative) 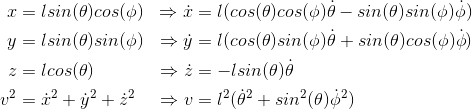The potential energy is found to be $U = -mglcos(\theta)$, thus we find the Lagrangian to be 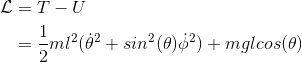The Euler-Lagrange (EL) equations yeild 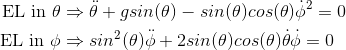Noting that the Lagrangian is indepent of $t$ and $\phi$ we find that energy and angular momentum in the $\phi$ direction are conserved 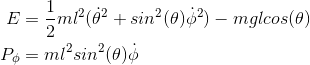In the simulation I solve this system of ODE's numerically, finding $\theta(t)$ and $\phi(t)$. From here $(x,y,z)$ can easily be found using the first 3 equations in the solution section.

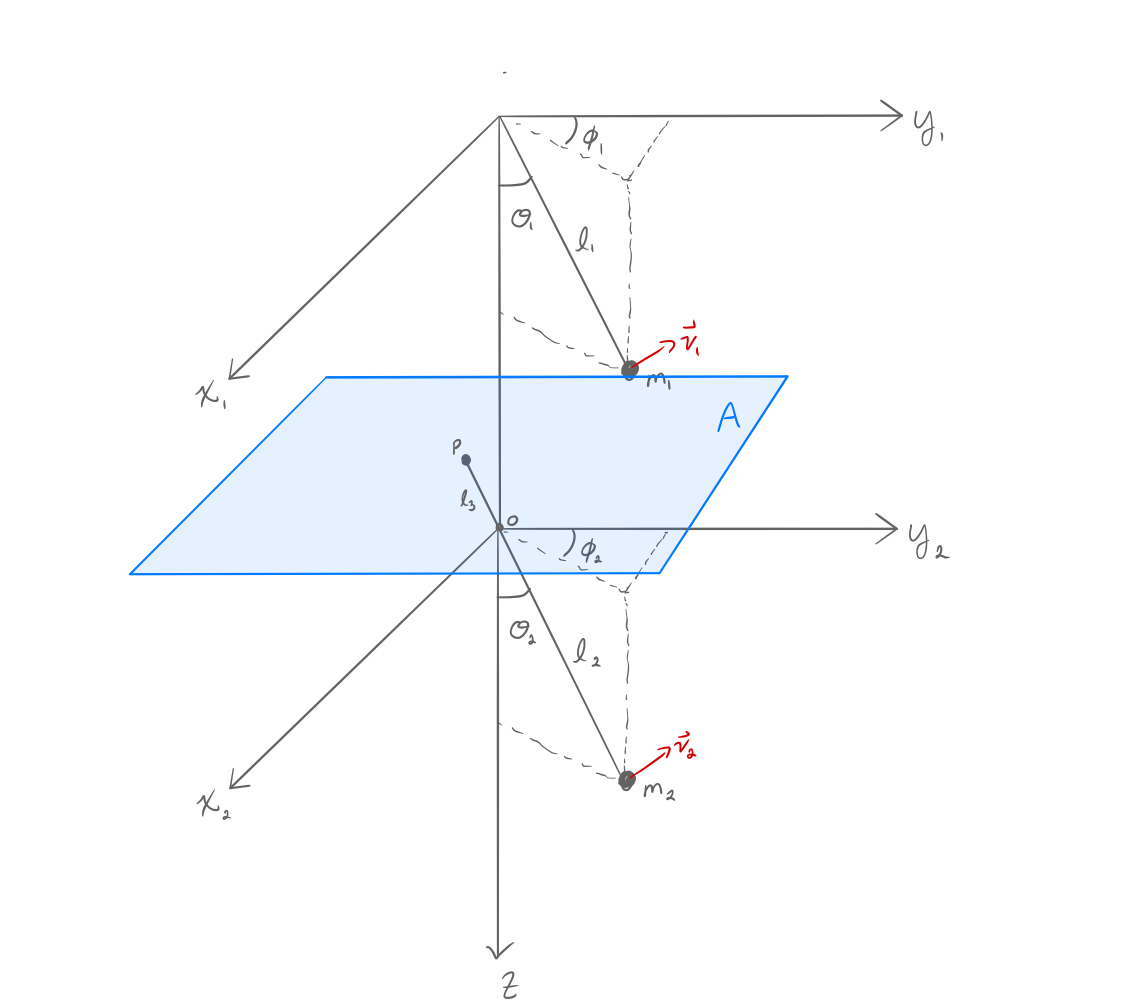
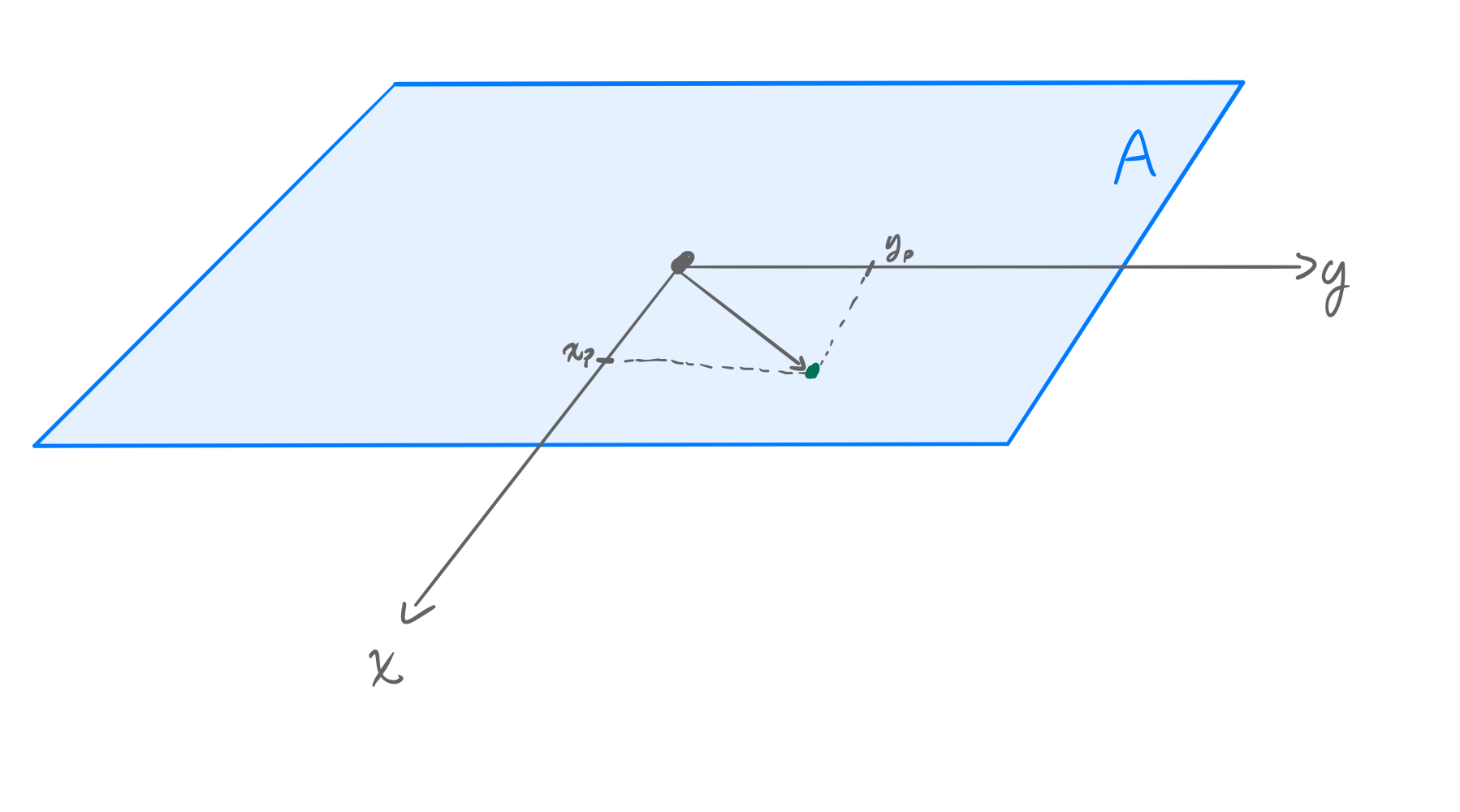
Now it is time to consider System 2, as mentioned the physics will behave exactly as calculated for System 1. System 2 will be accounted for by the translation of plane $A$ in the xy-direction. Here the $z$ translation doesn't need to be considered as I am taking the position of the falling ink to be the projection onto the $A$ plane (neglecting the velocity of the ink leaving the bottle). The translation of point $P$ (the origin of plane $A$) in the coordinate system for System 1 (and System 2) is 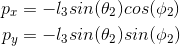By applying this transformation to the position of $m_1$ in from System 1 we can find the position where the ink will fall on plane $A$ which has $P$ as its origin. Thus the position of the ink drop on plane $A$ relative to origin $P$ will be 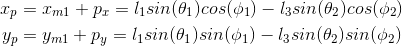Where $x_p$ and $y_p$ are defined as drawn in figure 4.

This is the equation that will govern the pattern drawn on $A$ for the complete system, which is plotted in the simulation.

To solve this problem the first step is to find the numerical solutions to the ODE's from the EL equations. From the conservation of angular momentum in $\phi$ we can note that 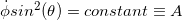which allows decoupling of the ODE's to give a single ODE 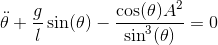We can then discretize this ODE to give 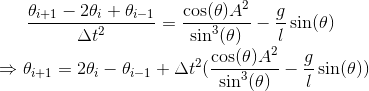where $\Delta{t}$ is a small time step. So if we know two initial positions, we can find all further positions. $\theta_0 = \theta(0)$ will be given as an initial condition, which just leaves the task to find $\theta_1 = \theta(\Deltat)$. This can be found by taking the 2nd order Taylor expansion about $\theta_{0}$ 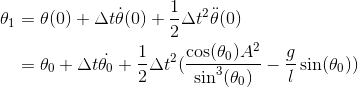Manipulating 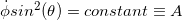and discretizing gives 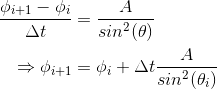This means we now have the equations that will allows a numerical solution. Notice that in these equations there is singularity about $\theta = 0$, this occurs due to a centrifugal barrier and is a product of solving these in spherical coordinates. There is more complex numerical methods to eliminate this singularity but they are beyond the scope of this project. These equations will accurately represent the system as long as $\theta$ is not to small, which is sufficient for the art I am trying to produce!

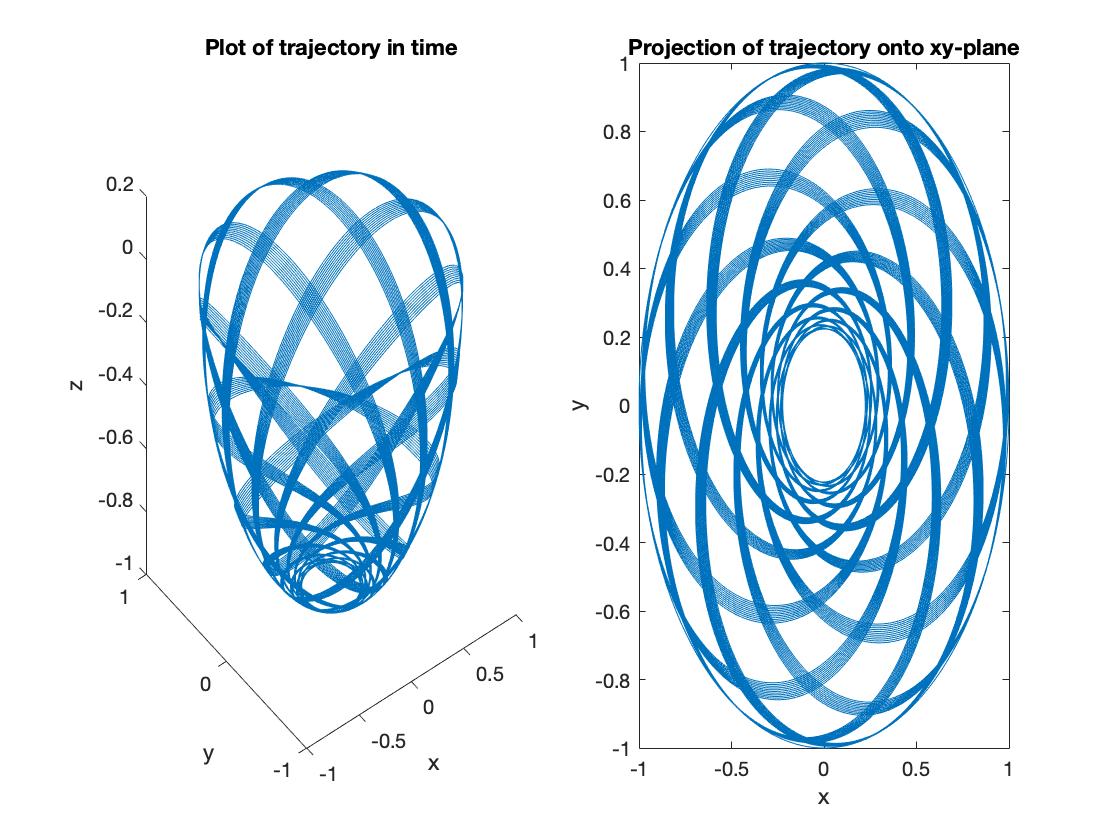
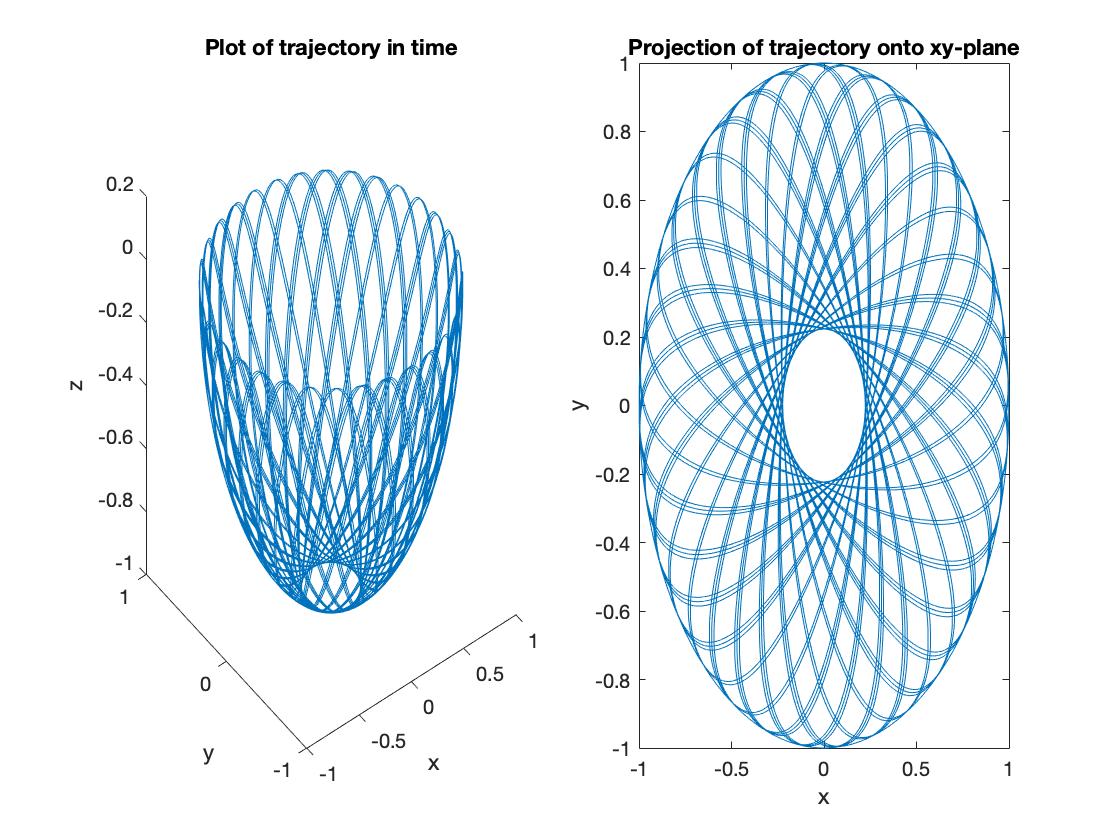
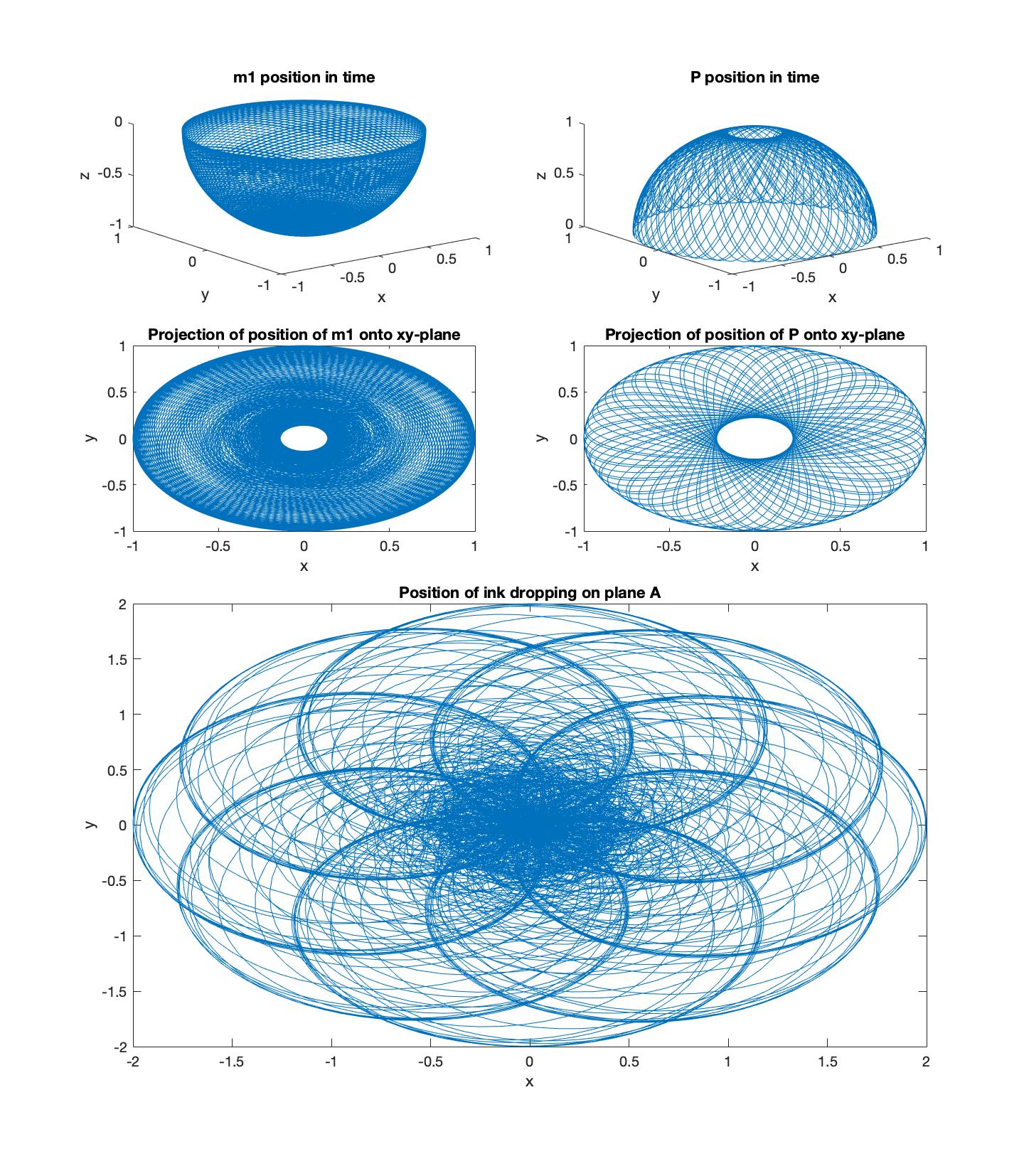
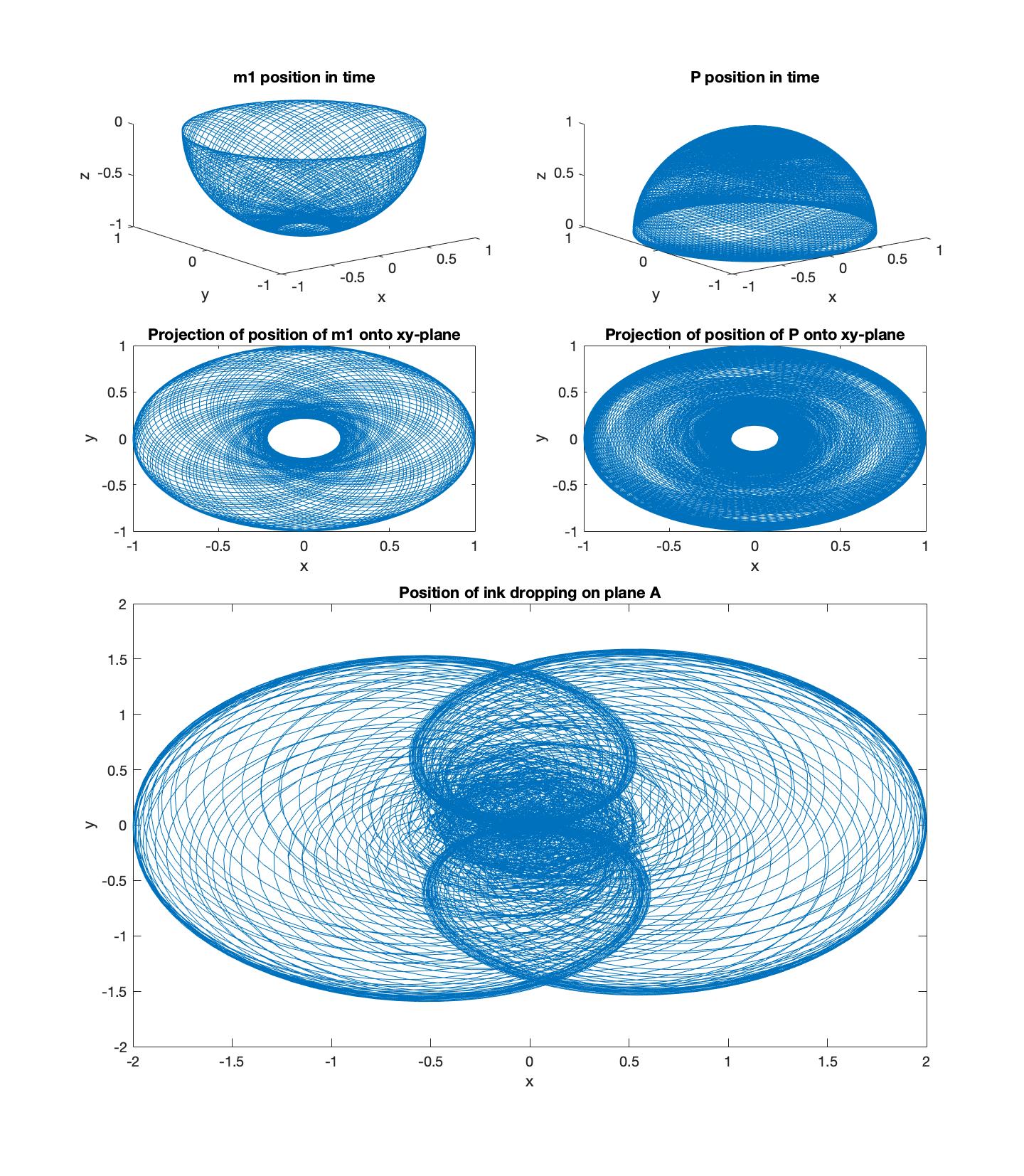
To solve these equations we will need to be provided 4 initial conditions . I want to demonstrate how the plots look in 3D and the projection onto a 2D surface which would be the art produced if A is held fixed. To do so I implemented this algorithm and plotted for a few different initial conditions in Matlab, results can be seen in Figure 5. You can find the code on my github.

Now all that is left is to add in System 2, thankfully we can use the exact same discretized equations to solve for $\theta_2, \phi_2$ which allow us to solve for $(p_x, p_y)$ and what we really need $(x_p, y_p)$ which are the positions of the ink within plane A.

Below are a few of the nice results that I produced